Применение ит в обработке медицинских изображений

метки: Изображение, Регистрация, Линия, Медицинский, Объект, Точка, Алгоритм, Скелет

Существует ряд алгоритмов позволяющих построить бинарный 3D скелет. Но из-за особенностей медицинских изображений таких как зашумленность, большие расстояния между слоями, геометрические и оптические искажения, нечеткие границы объектов, динамическое изменение объектов, с их помощью нельзя построить устойчивые к шумам средние линии. К тому же в случае исследования лучевыми методами много информации получают на основе данных плотности ткани. Поэтому при построении скелета сосудов желательно учитывать полутоновые свойства. Для решения этой задачи разработан алгоритм полутонового утоньшения, позволяющий построить образ сосудистой системы для дальнейшего анализа. В основе построения скелета сосудов лежит алгоритм псевдодистанционной карты [1].

Псевдодистанционная карта позволяет выполнить оценку расстояний между вокселями изображения и определить общие топологические свойства изображения. Локальные максимумы составляют основу для построения скелета такого изображения. В образовании скелета не участвуют приграничные локальные максимумы, которые удаляются по условию проверки близости границы, размеров и направления. Оставшиеся локальные максимумы образуют квазискелет, который исключает топологические особенности, связанные с неровностью границ и обладает большей устойчивостью к масштабированию и повороту.

1.1 Общая схема обработки изображений

Полезно разделить весь процесс обработки изображений на две большие категории: методы, в которых на входе и на выходе имеются изображения, и методы, где на вход поступают изображения, а на выходе возникают признаки и атрибуты, выделенные на основании этих изображений.

Эта схема не подразумевает, что к изображению применяется каждый из описанных процессов.

Регистрация изображения – первый из процессов, показанных на Рис.1. Регистрация может оказаться предельно простой, как в случае, когда исходное изображение уже представлению в цифровой форме. В общем случае стадия регистрации изображения включает некоторую предобработку, например, масштабирование.

Улучшение изображения входит в число наиболее простых и впечатляющих областей цифровой обработки изображений. По существу, за методами улучшения изображений стоит идея выявления плохо различимых деталей или просто подчеркивания интересующих характеристик на исходном изображении. Известным примером улучшения является усиления контраст изображения, потому что в результате «оно выглядит лучше». Важно иметь в виду, что улучшение качества – весьма субъективная область в обработке изображений.

Защита авторских прав на цифровое изображение

... РФ. Однако возникновение фотографии и рост ее популярности на протяжении XIXвека стали вызовом для авторского права. Поначалу юристам представлялось, что фотографическое изображение не должно признаваться объектом авторского права, так как причиной ...

Восстановление изображений – это область, также связанная с повышение визуального качества изображения, однако, в отличие от собственно улучшения, критерии которого субъективны, восстановление изображения является объективным в том смысле, что методы восстановления изображений опираются на математические или вероятностные модели искажений изображения. Напротив, улучшение изображений основано на субъективных предпочтениях человеческого восприятия, которые связаны с тем, что именно считается «хорошим» результатом улучшения.

Обработка изображений как этап следует отделять от понятия обработки изображении как весь процесс изменений изображения и получения некоторых атрибутов. Сюда может включатся и вейвлетная обработка (для представления изображений с несколькими степенями разрешения одновременно) и морфологическая обработка (связана с инструментами для извлечения таких компонент изображения, которые могут быть полезны для представления и описания формы).

Сегментация разделяет изображение на составные части или объекты. В целом автоматическая сегментация принадлежит к числу самых трудных задач цифровой обработки изображений. Излишне подробная сегментация уводит процесс решения задачи обработки изображения на сложный путь, если требуется идентифицировать объекты по отдельности. С другой стороны, недостаточно подробная или же ошибочная сегментация почти неизбежно приведет к возникновению ошибок на финальной стадии обработки.

Представление и описание почти всегда следуют непосредственно за этапом сегментации, на выходе которого обычно имеются лишь необработанные данные о пикселях, которые либо образуют границу области (т.е. дается множество пикселей, отделяющих одну область изображения от другой), либо представляют все точки самих областей. В обоих случаях необходимо преобразовать данные в форму, пригодную для компьютерной обработки. Первое решение, которое следует принять – должна ли эти данные представляться в форме границ областей или областей целиком. Представление границами подходит для тех случаев, когда в центре внимания находятся внешние характеристики формы областей, например, углы и изгибы. Представление областями более уместно, если акцент делается на внутренних свойствах объектов, например, текстуре или форме скелета. В некоторых приложениях эти представления дополняют друг друга. Выбор способа представления – лишь часть принятия решения по преобразованию «сырых» пиксельных данных в подходящую для дальнейшей компьютерной обработки форму. Должен быть еще указан метод описания данных, при котором бы выдвигались на передний план интересующие признаки. Построение описания, иначе называемое выбором признаков, связано с выделением атрибутов, которые бы выражали интересующую количественную информацию или бы моги служить основой для различения классов объектов.

Распознавание представляет собой процесс, которые присваивает некоторому объекту идентификатор (например, «бедренная кость») на основании его описателей.

Рассмотрим взаимосвязь между базой знаний и модулями обработки. На самом деле, знание о проблемной области, т.е. база знаний, некоторым образом закодировано внутри самой системы обработки изображений. Это знание может быть очень простым, как детальное указание участков изображения, где должна находиться интересующая информация, что позволит ограничить область поиска. База знаний может быть и очень сложной, как, например, взаимосвязанный список всех наиболее вероятных дефектов в задаче контроля материалов, либо база данных спутниковых изображений некоторого района с высоким разрешение в прикладных задачах обнаружения изменений, происходящих в этом районе. Помимо того, что база знаний руководит работой каждого модуля обработки, она также управляет взаимодействием между модулями. Эта отличительная особенность показана на рис. 1 с помощью двунаправленных стрелок между обрабатывающими модулями и базой знаний.

Интеллектуальные информационные технологии в экономической области

... управлении ресурсами, реинжиниринге, создании ситуационных центров. Все более заметно внедряются интеллектуальные информационные технологии аналитической обработки больших массивов информации, технологии поддержки решений. В 1990;х годах в совокупности и взаимосвязи развиваются: ...

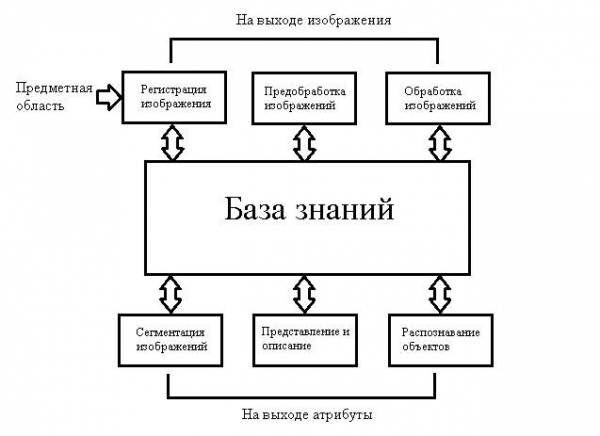
Рисунок 1 – Основные стадии цифровой обработки изображений

1.2 Особенности медицинских изображений

Существует несколько различных видов медицинских изображений, отличающихся как по способу получения и области применения, так и по особенностям конечного изображения. Ниже перечислены основные типы медицинских изображений.

Ангиографией является отображение тока крови по артериям и венам тела. До появления магниторезонансной терапии ангиография проводилась единственным способом. Для увеличения контраста сосудов в кровь человека вводилось рентгеноконтрастное вещество. Сосуды на ангиографических изображениях представляют собой сложные протяженные объекты с меняющимся контрастом. Поэтому основным механизмом в обработке и анализе таких изображений, позволяющим сохранить топологические свойства сосудов, является полутоновое утоньшение.

Ультразвуковые изображения – это полутоновые изображения, которые синтезируются с помощью отраженных ультразвуковых волн. Получение этих изображений основано на способности ультразвука проникать внутрь органа и взаимодействовать с тканью. Информация о структуре органа кодируется с помощью отраженных ультразвуковых волн. Ультразвуковые волны преломляются и отражаются в основном на границах регионов, которые имеют различные акустические характеристики. Современные сканеры оснащены гироскопом и позволяют отслеживать направление луча, что позволяет строить трехмерные изображения.

Гистологические изображения – цветные изображения гистологических срезов, сфотографированных с оптическим увеличением в 100-1000 раз. Объектами гистологического анализа являются фрагменты клеток и клеточных структур. Существует несколько способов получения 3D гистологических изображений, но самым распространенным является конфокальная микроскопия, которая позволяет получить объемные изображения клеточных образований и фрагментов ткани. Основным недостатком конфокальной микроскопии является изменения освещенности объекта в различные промежутки времени.

Компьютерная томография измеряет плотность ткани посредством ослабления рентгеновских лучей. Однако компьютерная томография характеризуется большим количеством проекционных изображений. Именно по ним строится томограмма, полностью отражая пространственные свойства исследуемого объекта. Использование проекций дает ряд преимуществ по сравнению с рентгеновскими снимками. Прежде всего, это возможность построения трехмерной модели объекта, объекты могут быть отделены друг от друга, можно получить срез практически в любой области. Однако расстояние между полученными слоями гораздо больше расстояния между соседними пикселями слоя, что приводит к необходимости реконструкции пропущенных данных.

1.3 Формальная постановка задачи

имеют несколько различных математических определений, содержащихся в технической литературе. Эти определения аналогичны для непрерывных пространств, но обычно приводят к разным результатам в дискретных пространствах.

В двумерном случае средняя линия [2] фигуры это множество кривых, определяемых как геометрическое место точек, которые имеют, по крайней мере, две ближайшие точки границы фигуры [3].

В трехмерном случае, соответствующий объект называется средней (или медиальной) плоскостью (Рис. 2).

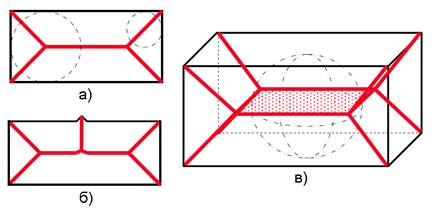
Рисунок 2 – а) Средняя линия в двухмерном случае б) Пример влияния граничных шумов на конечный результат, в) средняя плоскость в трехмерном случае

Наиболее наглядное определение средней линии дается через точки гашения в модели распространения огня, где граница фигуры сделана полностью из сухой травы, которую подожгли и средняя линия состоит из множества точек, где огни разных фронтов встречаются и гасят друг друга [2].

Также средние линии могут определяться как геометрическое место центров максимальных шаров (или дисков в двухмерном случае) [4].

Более формально, положим – трехмерный объект. Шар радиуса r с центром в точке определяется как , где – расстояние между двумя точками x и y в . Шар называется максимальным, если для него не существует шара большего радиуса, принадлежащего объекту, полностью содержащего [5].

Основное неудобство средних линий состоит в чувствительности к небольшим изменениям границ объекта [6][7].

Пример, приведенный на рис. 2(б), наглядно демонстрирует, как малые изменения границ приводят к большим изменениям средней линии.

2.1 Свойства средних линий

В этом пункте рассматриваются различные свойства средних линий, которые были получены путем анализа литературы и различных приложений скелетов в компьютерной графике и визуализации.

Гомотопность

Средние линии должны быть топологически эквивалентны исходному объекту [4][8].

Сохранение топологии может быть сформулировано следующим образом: Два объекта имеют одинаковую топологию, если они имеют одинаковое число связных компонент и полостей.

Однако для средних линий отсутствует понятие полости (из-за одномерности).

Поэтому в [10] было предложено следующее определение гомотопности: Скелет сохраняет топологию исходного объекта, если он содержит то же самое число связных компонент и имеет по крайней мере одну петлю для каждой полости в исходном объекте.

Циклы в скелете могут быть найдены с помощью алгоритма поиска в глубину, а наличие полостей в исходном объекте можно определить, используя метод, предложенный в [9].

Инвариантность относительно изометрических преобразований

Обозначим изометрическое преобразование (преобразование, в котором сохраняются расстояния между точкам) через T , рассматриваемый объект через O, объект, подвергшийся преобразованию T ( O ) , а его скелет должен быть таким же, как и трансформированный скелет исходного объекта, т.е. критерий инвариантности можно переписать

(2.1)

Это свойство очень важно для приложений, где средние линии используются для описания объекта.

Восстанавливаемость

В [11][12] рассматривают способность некоторых скелетов восстанавливать исходный объект из скелета. Учитывая определение средних линий как множества центров максимальных вписанных шаров, очевидным решением восстановления является вычисление и хранение для каждой точки скелета расстояния до ближайшей точки границы. Если обозначить функцию восстановления через , тогда точное восстановление означает

(2.2)

Трехмерный объект может быть полностью восстановлен из его представления средними линиями. Это свойство часто используется в приложениях для сжатия объектов, а также для визуализации [13].

В тоже время в общем случае, полное восстановление из-за дискретности множества вокселей не всегда возможно.

Толщина

Желательно, скелет должен быть одномерным, т.е. шириной в один воксель во всех направлениях, исключая точки сочленения различных ветвей.

Можно выделить три типа точек скелета [22]: регулярные точки, которые имеют ровно два соседних вокселя; конечные точки, имеющие ровно один соседний воксель, и точки соединения, которые могут иметь три или более соседей.

Тонкость и восстанавливаемость являются двумя противоречащими друг другу свойствами. Даже для объектов, в средних поверхностях которых фактически содержатся только кривые (например, для трубчатых объектов), скелет шириной в один воксель может не содержать все необходимые центры максимальных шаров для точной реконструкции объекта.

Центрированность

Важной характеристикой средней линии является его центрированность в пределах объекта. Для достижения идеальной центрированности необходимо, чтобы средняя линия находилась на медиальной поверхности, а сама медиальная поверхность была сосредоточена в пределах объекта. Кроме того, требуется, чтобы средняя линия находилась по центру медиальной поверхности [10].

Это свойство очень важно в приложениях сжатия изображений, а также в некоторых научных приложениях, например, в вычислении средней линии вихря [11]

Тем не менее, в большинстве случаев, точной центрированности извлеченного скелета не требуется или нежелательно (с учетом известной чувствительности скелета к малым возмущениям на границе объекта) [6] [7].

Приближенной центрированности достаточно для многих приложений, таких как виртуальная навигация или визуализация. Например, в виртуальной колоноскопии, надежность (см. ниже) и гладкость пути более важны, чем точная центрированность [14].

Покомпонентная дифференциация

С помощью средних линий можно различать различные компоненты исходного объекта, т.е. логические компоненты объекта должны быть биективны логическим компонентам средних линий.

Покомпонентная дифференциация отличается от гомотопности в том, что она касается логического восприятия составных частей единого объекта, в то время как последняя связана с геометрической составляющей компонентов, образующих различные объекты.

Проверка, удовлетворяет ли скелет этим свойствам, является сложной задачей, так как определение компоненты объекта не является достаточно точным, а определяется с участием человеческого восприятия, которое по своей сути субъективно.

Связность

Это свойство является следствием гомотопии. Если средняя линия соответствует односвязной компоненте, то она должна быть связной.

Помехоустойчивость

Как показано на рисунке 2 (б), средняя линия очень чувствительна к небольшим изменениям на границе. Желательное свойство скелета – слабая чувствительность к шуму на границе объекта, то есть, скелет объекта без шума и скелет того же объекта с шумом должны быть аналогичны.

Гладкость

Гладкость не только эстетическое свойство, но на самом деле полезно в некоторых приложениях. Например, в виртуальной навигации, которая использует среднюю линию как путь прохода камеры. Путь должен быть как можно более плавным, чтобы избежать резких изменений в изображении.

Иерархичность

Средняя линия сложных объектов может отражать естественную иерархию сложных объектов [15].

Иерархический подход является полезным, поскольку он может создать набор средних линий разных сложностей, которые могут быть использованы в различных приложениях. В строгой иерархии, скелет на определенном уровне в иерархии содержит все средние линии слоев ниже в иерархии в качестве подмножества. Такая строгая иерархия полезна в приложениях с использованием различных разрешений.

2.2 Существующие алгоритмы выделения средних линий

Существует много различных алгоритмов выделения средних линий для двумерного и трехмерного случаев. Хотя некоторые из 2D алгоритмы распространяются на 3D, мы ограничиваем наше рассмотрение алгоритмов, специально предназначенных для трехмерного случая.

В современной литературе обычно используется схема классификации, в которой выделяются следующие классы [16]: основанные на топологическом утоньшении, на использовании дистанционных карт (поиск точек хребта), а также на использовании диаграмм Вороного. Тем не менее, существуют методы, которые принадлежат нескольким классам одновременно (например, методы, основанные на дистанционных преобразованиях, которые используют топологическое утоньшение для «обрезки» получившегося скелета).

Методы топологического утоньшения строят скелет путем удаления вокселей границы объекта до тех пор, пока не будет получена необходимая тонкость. Все утоньшающие алгоритмы функционируют в дискретных пространствах и основываются на концепте «простой» точки, введенной Morgenthaler в 1981 [17].

«Простая» точка [18] это воксель, который может быть удален без изменения топологии объекта. Важное свойство «простых» точек состоит в том, что они могут быть определены локально, то есть путем анализа локальной окрестности, что делает алгоритмы топологического утоньшения более эффективными.

Процесс утоньшения начинается от границы объекта и продолжается, пока не останется «простых» точек. На каждой итерации, каждый граничный воксель проверяется на принадлежность множеству «простых» точек. Условия обычно реализованы как шаблоны (или маски) размера 3x3x3 или более. Центр маски совмещается с рассматриваемым вокселем и анализируется окрестность этого вокселя. Все воксели в маске имеют величины «0», «1» или «не опреден». Величина «0» соответствует вокселю границы, «1» – вокселю объекта, «не определен» может принадлежать как границе, так и объекту.

В то же время, удаление всех «простых» точек объекта приводит к укорочения самого скелета, потому что концевые точки скелеты сами являются «простыми».

Существуют несколько подклассов утоньшающих алгоритмов, различающихся по способу определения «простых» точек, а также порядком их удаления.

методы направленного утоньшения

методы последовательного утоньшения подполей

полностью параллельные методы

На рисунке 3 представлен пример топологического утоньшения.

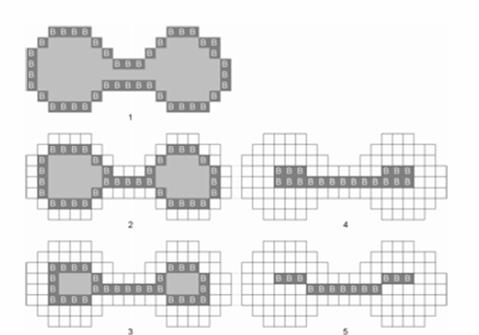
Рисунок 3 – Пример алгоритма утоньшения для двумерного случая. Граничные точки, помечаются «B» и затем удаляются, если они «простые»

Дистанционное преобразование – преобразование, которое каждой точке изображения ставит в соответствие расстояние в заданной метрике до ближайшей точки фона (Рис. 4).

Формальная запись:

,

(2.3)

где – некоторая метрика.

Алгоритмы для построения карт расстояний могут быть классифицированы по нескольким критериям.

Классификация по способу вычисления расстояния:

Чамферные дистанционные преобразования [24], где новое значение расстояния для вокселя вычисляется из расстояний его соседей и соответствующих весов маски.

• Векторные дистанционные преобразования [25], в котором для каждого обработанного вокселя хранится вектор ближайших точек границы, а для необработанного вокселя этот вектор строится, используя вектора соседей из шаблонной окрестности.
• Дистанционные преобразования на основе решения эйконального уравнения [26], где расстояние находится из конечных разностей первого или второго порядков расстояний соседних вокселей
• Квадратное евклидово дистанционное преобразование [27], в котором вместо расстояния до ближайшей точки фона хранится квадрат этого расстояния, что позволяет воспользоваться некоторыми преимуществами.

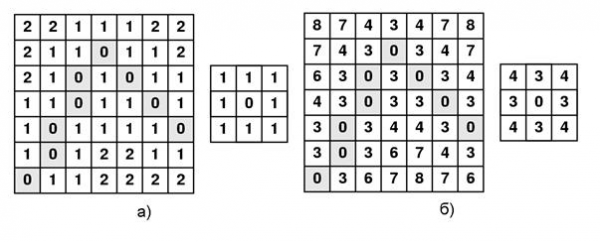
Рисунок 4 – Дистанционные карты с использованием а) шахматной метрики

б) (3,4)-метрики Чамфера

Хребтовые точки дистанционной карты соответствуют вокселям, которые находятся в центре объекта. Они выступают в качестве потенциальных кандидатов точек средних линий. Ниже перечислены некоторые подходы, использующиеся для поиска вокселей-кандидатов:

методы утоньшения

методы поиска градиента

методы вычисления дивергенции

методы адаптивного утоньшения

Множество вокселей-кандидатов обычно имеет большую размерность и следующий шаг как правило заключается в уменьшении их количества.

Для связности большинство алгоритмов используют минимальные остовные деревья [32], кратчайшие пути [33] или другие алгоритмы на графах.

Некоторые методы сначала используют объединение, затем удаление вокселей путем нахождения кратчайшего пути в связанном множестве [29].

Основное преимущество этих методов в том, что вычисление дистанционной карты происходит очень быстро (за линейное время от числа вокселей), что очень важно во многих приложениях.

Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек более близких к одному из элементов множества S, чем к любому другому элементу множества [41].

Пример диаграммы Вороного продемонстрирован на рисунке 5.

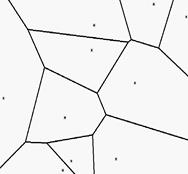
Рисунок 5 – а) 10 сгенерированных точек и б) построенная для них диаграмма Вороного.

Популярный подход состоит в использовании диаграмм Вороного [34], порожденых вершинами трехмерной полигональной сетки или непосредственно точками границы. Внутренние ребра и грани диаграммы Вороного, могут быть использованы для выделения средних линий и плоскостей. Средняя линия может быть получена из медиальной плоскости путем утоньшения последней. В работе [35], определяется число «шаровых областей » (непересекающихся максимальные шары), центры которых позднее объединеняются в среднюю линию, используя информацию медиальной поверхности. В работе [36], средняя линия рассчитывается путем морфологической эрозии диаграмм Вороного на основе геодезической функции.

Кроме дистанционных карт могут использоваться другие типы карт, построенные с помощью функций, отличных от функции расстояния.

В этот класс включена обобщенная потенциальная функция поля [37] [38] [15], где потенциал во внутренней точке объекта определяется как сумма потенциалов, возникающих на границе объекта. В дискретном случае [15], граничные воксели считаются точечными зарядами, генерирующими потенциальное поле. Функция электростатического поля используется в [38] для создания потенциала внутри объекта. Также используется частный случай потенциального поля – сила отталкивания – в работах [37] [38] и [15] (Рис. 6).

Скелет строится через определение локальных экстремумов построенного поля и объединения их.

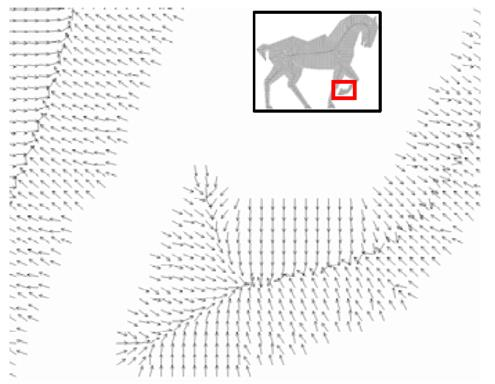
Рисунок 6 – Поле сил отталкивания двумерного изображения.

Локальные экстремумы могут быть найдены за счет критических точек векторного поля [15] или обнаружения локальных максимумов вдоль эквипотенциальных контуров [2].

Другие методы непосредственно используют «силовые» алгоритмы, начиная в нескольких стартовых точках («семенах») и используя тот факт, что вычисляемые силы затухают в пиковых точках.

Основным преимуществом этих функций перед функцией расстояния является то, что они могут выделять сглаженные линии на медиальных поверхностях. Это происходит потому, что они принимают во внимание большие приграничные районы, а не только ближайшие точки на границе. Это также создает эффект усреднения, который делает эти алгоритмы менее чувствительны к шумам на границе. Тем не менее, вычислительная сложность у них гораздо выше.

2.3 Сравнение существующих методов

В этом пункте рассмотрены различные подходы к построению средних линий и их воздействие на различные свойства, описанные в пункте 2.2.

Гомотопность

Алгоритмы утоньшения обеспечивают гомотопность, поскольку удаляются только те воксели, которые не меняют топологию объектов.

Поскольку методы, основанные на дистанционных картах, не выделяют скелет напрямую, сохранение топологии зависит от последующих шагов – обрезки и связывания. Очевидно, что алгоритмы, основанные на минимальных остовых деревьях не сохраняют топологию, потому что они не могут создавать петель.

Средние линии, построенные алгоритмами, основанными на общеполевых методах, могут быть несвязными даже для односвязных объектов [15], так как этот класс алгоритмов сильно зависит от разрешения изображений, а также от погрешностей при вычислениях.

Инвариантность при изометрических преобразованиях

Направленные методы утоньшения чувствительны к ориентации объекта. Окончательный результат (конечные точки, число ветвей и их местоположение) зависит от порядка, в котором обработаны различные направления. Дистанционные карты, диаграммы Вороного и методы, основанные на характеристиках полей, не зависят от ориентации объекта.

Во всех случаях, затрагивающих дискретные представления объектов, конечное представление воксельной сетки допускает небольшую погрешность при преобразовании объектов. В результате даже при том, что алгоритмы выделения средних линий не чувствительны к ориентации, сами входные данные уже несут некоторую погрешность из-за преобразования. Эта погрешность обнаруживается на границе преобразованного объекта, и этот эффект подобен эффекту поверхностного шума.

Восстанавливаемость

Средняя линия или средняя поверхность трехмерного объекта захватывает локальное симметричное представление в объекте через различные типы элементов: участки поверхности в скелете представляют симметрические пластинчатые области исходной формы, в то время как отдельные кривые в скелете соответствуют цилиндрическим (трубчатым) областям формы. Очевидно, что независимо от используемого метода выделения, полная и точная реконструкция исходного объекта не возможна при наличии информации, сохраненной в одной только средней линии. Так как скелет содержит только сегменты кривой, плоские части объекта не могут быть восстановлены от него.

Цилиндрические формы (то есть, формы, которые могут быть точно представлены обобщенными цилиндрами), представляют специальный класс объектов, которые могут быть точно восстановлены от одного только скелета. Общие формы могут только быть приближены обобщенной цилиндрической реконструкцией. Ясно, что более плотный скелет кривой приведет к более точному результату. При восстановлении с помощью подхода наращивания шаров [31] необходима информация дистанционной карты для определения радиуса шара, который будет выращен из каждого вокселя скелета. В этом отношении, методы, основанные на дистанционных картах, имеют преимущество перед другими методами, потому что эта информация доступна.

Толщина

Алгоритмы утоньшения могут непосредственно построить тонкий скелет (при использовании утоньшающих шаблонов).

Параллельные алгоритмы утончения, которые удаляют все простые воксели сразу, возможно, не в состоянии достигнуть соответствующего представления из-за ограничений топологии. На рисунке 4 имеем прямоугольник, ширина которого четное число вокселей. На последнем шаге процесса утоньшения средняя линия будет шириной в 2 вокселя. Хотя все воксели этой кривой «простые» точки, удаляя их полностью, мы бы удалили всю среднюю линию. На данном этапе никакие другие «простые» точки не могут быть удалены, и скелет не представлен в 1D. У направленных методов утончения предусмотрена эта проблема: один ряд вокселей в средней линии будет удален, а второй ряд будет сохранен в последующих шагах.

Методы, основанные на дистанционных картах и диаграммах Вороного не представляют скелет в 1D. Для обоих методов необходима постобработка по уменьшению количества вокселей [39].

Центрированность

Алгоритмы утоньшения и методы полевых характеристик не гарантируют центрированность. В случае направленного утоньшения, центрированность зависит от порядка применения различных направлений. В случае общеполевых методов, которые рассматривают области, отличные от ближайших точек границы, центрированность также не гарантируется.

Методы, использующие дистанционные карты могут лучше достигать центрированности, потому что информация о центрах (максимальных шаров) включена в дистанционную карту.

Геометрические методы напрямую вычисляют контактные точки (точки, которых касаются границы максимальных вписанных сфер) также могут достигать центрированности.

Методы, основанные на диаграммах Вороного, зависят от выбора плотности поверхности объекта: плотный объект дает более отцентрированную среднюю линию, но увеличивает время работы. Проблемы с центрированностью возникают [39] особенно в регионах, где топология объекта изменяется между последовательными множествами уровней. Это также зависит от разрешения (расстояние между двумя последовательными множествами уровней).

Покомпонентная дифференциация

Способность различать различные компоненты средней линии зависит от способности обнаруживать точки сочленения, т.е. точки, в которых соединяются две или более линии.

Алгоритмы утоньшения непосредственно могут классифицировать обрабатываемые точки как точки сочленения.

Методы, основанные на дистанционных картах сами по себе не могут определять тип точек построенного скелета. Обычно данная классификация происходит на этапе постобработки [19].

Тем не менее, переход размещения для этих классов методов чувствителен к шуму.

Метод множеств уровня может также непосредственно определить точки сочленения (как центры построенных множеств уровней).

Связность

Связность обычно гарантируется всеми классами алгоритмов. Некоторые алгоритмы (утоньшения, алгоритм множеств уровня) явно поддерживают связность во время выполнения, тогда как для других необходима постобработка.

Надежность

Алгоритмы утоньшения, а также алгоритмы, основанные на дистанционных картах и диаграммах Вороного, чувствительны к шумам и генерируют много ненужных ответвлений в скелете. Некоторые подходы используют постобработку получившихся скелетов [28].

Общеполевые подходы менее восприимчивы к шуму из-за большого количества включенных усредняющих основных вычислений. Эти методы являются более чувствительными к разрешению, поскольку средняя линия в объектах может привести к неустойчивости в численных расчетах.

Многие из этих алгоритмов, описанных в литературе, как правило, иллюстрируется лишь несколькими примерами и не протестированы на большой базе данных общих 3D объектов (например, базы данных 3D-моделей [40]).

Таким образом, остается неясным, как надежны в целом эти алгоритмы в отношении выбора их параметров.

Гладкость

Из-за дискретного характера объектов, алгоритмы утоньшения не дают плавных средних линий.

Методы, основанные на дистанционной карте, на местах имеют тот же недостаток, потому что в процессе построения карты нет усреднения. Однако в дальнейшем, при обрезке и связывании, можно включать некоторые алгоритмы сглаживания. Алгоритмы на основе диаграмм Вороного ведут себя подобным образом.

В случае общеполевых методов, усреднение используется при расчете векторного поля. Хотя в некоторых алгоритмах можно провести шаг постобработки, независимо от алгоритма выделения скелета, для сглаживания линий.

Иерархичность

Иерархичность (способность создавать семейства средних линий различной сложности), не достижима при использовании алгоритмов утоньшения, поскольку при воксельной обработке существует только два варианта: сохранить его или удалить его. Скелет получается только на последней итерации алгоритма.

Методы, основанные на дистанционных картах, могут быть иерархичными, варьируя число кандидатов-вокселей на шаге обрезки. Для того, чтобы получить скелет строгой иерархии (т. е. скелет одного уровня, входит полностью в скелет более высокого уровня), на шаге связывания необходимо принимать во внимание скелет предыдущего уровня.

Общеполевые методы также могут выделять иерархичные средние линии, варьируя количество исходных точек («семян»), используемых для построения отдельных сегментов средних линий.

Эффективность

Алгоритм топологического утоньшения – практически линейный процесс относительно числа вокселей объекта. Большинство вокселей входного объекта удаляются, когда они обрабатываются впервые (в качестве «простых» точек); «непростые» точки обрабатываются повторно. Сложность анализа таких алгоритмов затруднено, так как конечный результат зависит от входных данных.

Дистанционная карта может быть построена также за линейное время. Последующие шаги обрезки и стыковки могут иметь большую сложность, однако, они оперируют гораздо меньшим множеством вокселей.

Вычислительная сложность построения диаграмм Вороного для множества из n точек в худшем случае , хотя на практике она почти линейна [4].

Как и в случае с дистанционными картами, здесь необходима постобработка.

Сложность вычисления потенциального поля [15], где n – общее число вокселей. Для больших объектов или объектов с высоким разрешением этот метод работает очень долго.

Краткие выводы

В таблице 1 для каждого класса алгоритмов представлены достигаемые или недостигаемые свойства. «Да» означает то, что класс алгоритма гарантирует сохранение того или иного свойства, «Нет» в противном случае. Пустые места оставлены, если свойство сохраняется только некоторыми алгоритмами в классе или в случае, когда свойство слишком сложно для анализа подхода определенного класса (как было показано выше)

Таблица 1 – Свойства, достижимые различными классами алгоритмов.

Свойство	Утоньшение	Дистан-ционные карты	Диаграммы Вороного	Обще-полевые методы
Гомотопность	Да	Да	Нет
Инвариантность	Да	Да
Восстанавли-ваемость	Нет	Нет	Нет
Тонкость	Да
Определение сочленений	Да	Да
Связность	Да
Надежность	Нет	Нет	Нет	Да
Гладкость	Да
Иерархичность	Нет	Да
Эффективность	Да	Да	Да	Нет

Глава 3 Практическая реализация

3.1 Архитектура и состав системы

В ходе выполнения работ была предложена оригинальная концепция реализации как функций анализа данных компьютерной томографии так и функций взаимодействия с пользователем (медицинским специалистом).

Таким образом, разрабатываемый программный комплекс представляет собой симбиоз технологий и программных решений, позволивших изящно обойти возникшие проблемы. Одной из таких проблем является риск неэффективности или малой востребованности разработанного функционала по обработке и анализу изображений в реальных клинических условиях. С этой проблемой связана другая задача: как сделать универсальный интерфейс, понятный для неспециалиста в области программной инженерии.

В настоящее время существует ряд популярных среди программистов комплексов с открытыми исходными кодами, и доступными динамически подключаемыми библиотеками, позволяющими унифицированно решить вопрос о реализации базовых (и не только) функций работы с сериями изображений компьютерной томографии. Однако, в силу быстрого развития медицинской техники, такой подход порождает еще одну проблему – проблему совместимости, корректной организации оперативной памяти и быстрой реализации функций чтения новых форматов, содержащих с точки зрения универсальных библиотек избыточную «незнакомую» информацию. В этом разделе приведены результаты исследований и программного решения описанных проблем.

Организация программной части должна быть ориентирована на задачи, решаемые автоматизированным комплексом микроскопических исследований, а именно:

• улучшение и обработка статических и динамических изображений,
• анализ изображений и выделение информативных областей на них,
• получение значений перечня наиболее важных параметров в соответствии с протоколом исследования,
• сохранение текстовой и графической информации, полученной в ходе проведённого исследования.

В соответствии с поставленными задачами, в программном пакете должны присутствовать следующие блоки, объединённые внутренней логической связью:

• блок ввода и предварительной обработки изображений,
• блок анализа полученного изображения, сегментации и идентификации информативных областей на нём.
• блок расчёта значений параметров и характеристик, выбранных из списка в соответствии с протоколом конкретного исследования

Первый блок, отрабатывает технические задачи по получению компьютерного варианта исследуемого изображения необходимого уровня качества. Определяющим же в этом списке является третий блок. Именно в нём должны быть указаны параметры, по которым будут строиться алгоритмы работы второго и четвёртого блоков. Именно поэтому, выработку требований к программному продукту следует начать с третьего блока, а точнее с рассмотрения вариантов математического описания признаков и характеристик наноскопических объектов, определённых в соответствии с протоколами исследования.

Для построения структурной схемы взаимодействия базового программного обеспечения проведена оценка функциональности и совместимости существующих средств и данных программной разработки, задач, решаемых разрабатываемым программным обеспечением, исходные данные, признаки и характеристики исследуемой поверхности материала при наноскопическом увеличении.

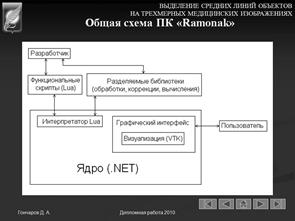
Логические связи и функциональные узлы программного блока приведены на рисунке 7.

В основе работы программного блока анализа изображений лежит функционирование четырех библиотек:

1) для работы с изображением, обеспечивающее доступ к изображению и его элементам, возможность контроля и изменения его характеристик,

2) для предобработки изображения, включая функции улучшения, фильтрации, контрастирования и т.д.

3) для работы математической морфологии выделения и коррекции объектов, включающая аппарат для коррекции формы объектов,

4) для вычисления характеристик, состоящая из набора параметров, и функции анализа и обслуживания сервисов вычисления характеристик по параметрам.

На рисунке 7 представлена общая схема взаимодействия базового программного обеспечения.

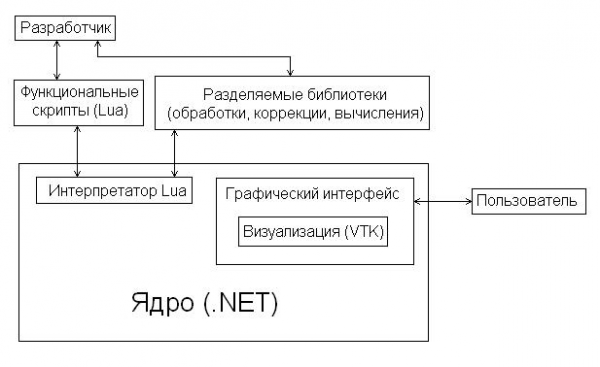
Рисунок 7 – Структурная схема взаимодействия базового программного обеспечения

В качестве основного модуля обеспечивающего взаимодействие элементов комплекса должен быть разработан интерпретатор внутреннего языка программирования. Данный модуль включает графический интерфейс, глобальные переменные, структуру изображения. Построение графического интерфейса осуществляется посредством подключения библиотек. Разработка новых элементов интерфейса комплекса может осуществляться как за счет текстового программирования в интерпретаторе, так и с помощью графических инструментальных средств.

Структуру изображения определяет модуль графического интерфейса, который отвечает за визуализацию изображений. Заголовки структур изображения являются переменными интерпретатора. Модуль графического интерфейса также включает функции чтения и записи изображений, простые функции обработки и функции интерактивного построения контура. Все интерактивные функции возвращают значения в блок событий, который изменяет глобальные переменные интерпретатора. Этот модуль обеспечивает взаимодействие пользователя с комплексом. Он позволяет обрабатывать и анализировать несколько изображений. Добавление новых функций обработки и анализа осуществляется через группу функций разработчиков. Новые функции на входе могут получать любые глобальные переменные, хранящиеся в интерпретаторе, а также текстовые и числовые константы. Внутреннее управление комплексом осуществляется через скриптовые функции, которые делятся на две категории:

• обеспечивающие организацию графического интерфейса,
• отвечающие за оперативную функциональность и настройку комплекса.

Все скрипты хранятся в текстовом виде и легко доступны. Однако они не предназначаются для редактирования пользователем и могут быть отредактированы разработчиками для оперативного изменения функциональности комплекса или его настройки непосредственно на рабочем месте.

В основу программной оболочки и функций визуализации заложены библиотеки интерпретатора, визуализации и графического интерфейса программы, в котором определены способы разработки программных модулей и их взаимодействия. Комплекс использует базовый набор программных средств, обеспечивающий взаимодействие и работу программных модулей. Вызов окна графического модуля осуществляется посредством команды интерпретатора. Допустим одновременный вызов нескольких окон. Для осуществления взаимодействия модуля графического интерфейса с интерпретатором, модуль преобразован в DLL-библиотеку.

3.2 Взаимодействие с клинической АСУ

Как упоминалось выше, чтобы избежать проблемы свзязанные с совместимостью функционала чтения форматов хранения КТ-данных, в рамках работ по настоящему договору были разработаны и реализованы функции (табл.2 функций приведен ниже), позволяющие манипулировать DICOM-сериями, полученными с современных томографов и содержащих большой объем информации, также инициализирующие интеллектуальную обработку (выделение контуров).

Таблица 2 – Функции для работы с сериями КТ-данных

Вызываемая функция	Действие
int GetDCMPatienListCount ()		Получить количество доступных серий.
char ** GetDCMPatienList ()		Получить список серий пациента.
char** GetDCMFilesList (int seriesNumber)		Получить список всех файлов срезов из серии
char * GetDCMData (int seriesNumber)		Получить имя созданного файла с данными по всем слоям сканирования данной серии.
int GetDCMFileByteShift (int seriesNumber , int dcmFileNumber)		Получить сдвиг от начала данных по всем слоям сканирования (GetDCMData) для dcmFileNumber-го файла seriesNumber-й серии.
int GetDCMDataWidth (int seriesNumber , int dcmFileNumber)		Получить ширину среза в пикселях.
int GetDCMDataHeight (int seriesNumber , int dcmFileNumber)		Получить высоту среза в пикселях.
double[3] GetDCMDataPosition (int seriesNumber , int dcmFileNumber)		Получить 3D положение среза.
double[3] GetDCMDataResolution (int seriesNumber , int dcmFileNumber)		Получить 3D размер вокселя.
double[6] GetDCMDataOrientation (int seriesNumber , int dcmFileNumber)		Получить 3D ориентацию.
int GetDCMDataContoursCount (int seriesNumber , int dcmFileNumber)		Получить количество контуров у среза
int GetDCMDataContourPointsCount (int seriesNumber , int dcmFileNumber, int contourNumber)		Получить кол-во точек в контуре под номером contourNumber;
point* GetDCMDataContourPoints (int seriesNumber , int dcmFileNumber, int contourNumber)		Получить точки контурп под номером contourNumber.

3.3 Методика решения прикладных задач и демонстрация использования

Для того, чтобы загрузить изображения формата DICOM следует выбрать пункт меню File-Open DICOM или нажать комбинацию клавиш Ctrl+N (Рис. 9).

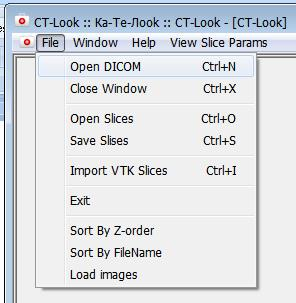
Рисунок 9 – Пункт меню открытия серии медицинских изображений.

После вызова пункта меню откроется диалог выбора файла. Следует указать любой файл серии слоев, которую необходимо загрузить (Рис. 10).

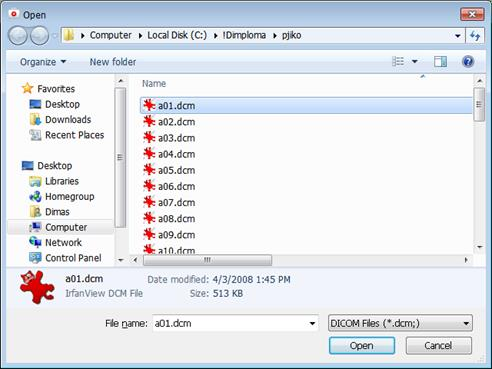
Рисунок 10 – Диалог выбора файлов.

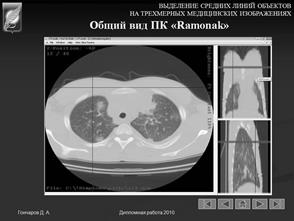
После выбора файла программа загрузит всю серию изображений и отобразит три проекции (аксиальную, корональную и сагиттальную) (Рис. 11).

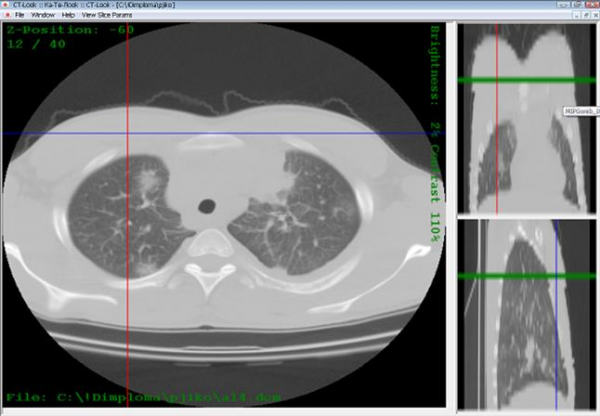Рисунок 11 – Общий вид программы.

Для выделения средних линий необходимо выбрать пункт меню Window-Extract skeleton (Рис. 12).

Рисунок 12 – Пункт меню выделения средних линий

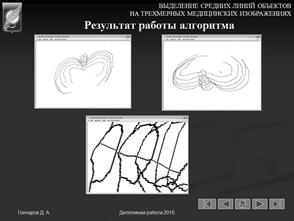
Результат выделения средних линий представлен на рисунке 13. Получившееся изображение можно вращать в различных направления, выбирать различное приближение.

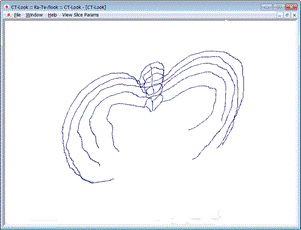
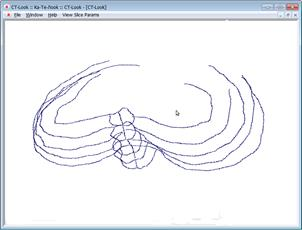
а) б)

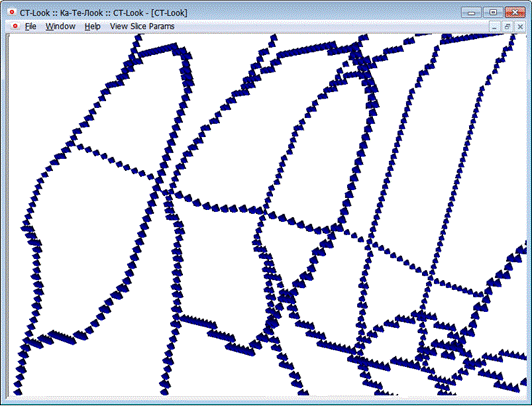
в)

Рисунок 13 – Пример построения скелета а) и б) различные ракурсы в) приближение

Заключение

В данной работе были изучены алгоритмы выделения средних линий на трехмерных изображениях и сравнены по многим критериям (сохранение топологии, инвариантность относительно преобразований, связность и т.д.).

Также был разработан алгоритм выделения средних линий, основанный на псевдодистанционных картах. Основным преимуществом данного метода является хорошая устойчивость к шумам, инвариантность относительно поворотов и масштабирования, скорость работы. Из недостатков стоит отметить большой объем используемой памяти, отсутствие возможности восстановления исходного объекта. Данный алгоритм реализован в рамках программного комплекса анализа изображений компьютерной томографии.

В ходе выполнения данной работы был подготовлен интерфейс взаимодействия комплекса анализа изображений компьютерной томографии с клинической автоматизированной системой управления. Также было разработано взаимодействие интерпретатора Lua с различными библиотеками обработки изображений и реализованы алгоритмы вычисления характеристик объектов для их использования в интерпретаторе Lua.

Список литературы к реферату

[Электронный ресурс]//URL: https://pravsob.ru/diplomnaya/registratsiya-meditsinskih-izobrajeniy/

1. Недзьведь А.М., Абламейко С.В., Белоцерковский А.М., Лемман Т. Быстрый метод выделения сети сосудов на полутоновых ангиографических изображениях. – Искусственный интеллект. 2, 2006, С. — 206-210.

2. H. Blum. A Transformation for Extraction New Descriptors of Shape, Models for the Perception of Speech and Visual Form, MIT Press, 1967.

3. W. Gong and G. Bertrand. A simple parallel 3D thinning algorithm. Proc. IEEE Pattern Recognition, 188-190, 1990.

4. A. Lieutier. Any open bounded subset of Rn has the same homotopy typethan its medial axis, Proc. ACM SMI, 2003.

5. T.Y. Kong, A. Rosenfeld. Digital topology: Introduction and survey. Comp. Vision, Graphics, and Image Proc., 48(3):357-393, 1989.

6. S.W. Choi, H.P. Seidel. Linear One-sided Stability of MAT for Weakly Injective 3D Domain, Proc. ACM SMA, 2002.

7. P.K. Saha, B.B. Chaudhuri. 3D Digital Topology under Binary Transformation with Applications, Computer Vision and Image Understanding, 63(3):418–429, 1996.

8. S. Svensson, C. Arcelli, G. Sanniti di Baja. Finding cavities and tunnels in 3D complex objects, Proc. ICIAP, pp. 342 – 347, 2003.

9. G. Sanniti di Baja, S. Svensson. A New Shape Descriptor for Surfaces in 3D Images, Pattern Recognition Letters, 23:703, 2002.

10. N. Gagvani and D. Silver. Parameter Controlled Volume Thinning, Graphical Models and Image Processing, 61(3):149-164, 1999.

11. C.W. Niblack, P.B. Gibbons, D.W. Capson. Generating skeletons and centerlines from the distance transform, Graphical Models and Image Processing, 54(5):420-437, 1992.

12. N. Gagvani and D. Silver. Animating volumetric models, Academic Press Professional 63(6):443-458, 2001.

13. D.-G. Kang, J.B. Ra. A New Path Planning Algorithm for MaximizingVisibility in Computed Tomography Colonography,

14. N. Cornea, D. Silver, X. Yuan, R. Balasubramanian. Computing Hierarchical Curve-Skeletons of 3D Objects, The Visual Computer, 21(11):945-955, 2005.

Предметный указатель к реферату

—А—

ангиография, 6

—В—

восстанавливаемость, 9, 17

—Г—

гладкость, 11, 19

гомотопность, 8, 16

—Д—

диаграмма Вороного, 15, 20

—И—

иерархичность, 11, 19

изображение

гистологическое, 7

медицинское, 3

ультразвоковое, 6

инвариантность, 9, 17

—К—

компьютерная томография, 7, 24

—М—

метод

общеполевой, 15

утоньшения подполей, 12

—Н—

надежность, 19

—П—

покомпонентная дифференциация, 10, 18

помехоустойчивость, 10

потенциальное поле, 20

преобразование

дистанционное, 11, 13, 20

псевдодистанционное, 29

чамферное, 13

псевдодистанционная карта, 3

—С—

связность, 10, 19

сегментация, 5

среданяя линия, 7

—Т—

толщина, 9, 17

топологическое утоньшение, 20

—У—

утоньшение, 3, 11

—Ц—

центрированность, 10, 18

Интернет ресурсы в предметной области исследования

1. – сайт Высшей аттестационной комиссии Республики Беларусь. Здесь собраны все нормативные акты, касающиеся оформления и защиты диссертаций.

2. http://www.medical-image-processing.info/ – cтатьи и файлы по алгоритмам обработки медицинских изображений.

3. ? – свободная база медицинских изображений.

4. – описание различных типов медицинских изображений.

5. – официальный Web-ресурс группы молодых ученых и разработчиков, которые создают интеллектуальные и прикладные, финансово-аналитические системы.

6. http://machine-learning.martinsewell.com/pattern-recognition – обширная библиография, посвященная распознаванию образов.

7. ftp://medical.nema.org/medical/dicom/2009/ – последняя спецификация формата DICOM.

8. http://www.jprr.org – сайт журнала «Journal of Pattern Recognition Research».

9. http://www.worldscinet.com/ijprai – сайт журнала «International Journal of Pattern Recognition and Artificial Intelligence».

10. http://www.aaai.org – сайт ассоциации «Association for the Advancement of Artificial Intelligence».

Действующий личный сайт в WWW

http://dzmitry-hancharou.narod.ru

Граф научных интересов

магистранта Гончарова Д.А. факультета прикладной математики и информатики

Специальность «прикладная математика и информатика»

Смежные специальности 05.13.11 — математическое и программное обеспечение вычислительных машин, комплексов и компьютерных сетей 1. Математическое и программное обеспечение систем искусственного интеллекта, мультимедиа, принятия решений, функционального и логического программирования, баз данных, знаний и экспертных систем. 05.13.15 – вычислительные машины, комплексы и компьютерные сети 2. Средства аппаратно-программной обработки изображений, включая распознавание образов, визуализацию информации, обеспечивающие высокую производительность и надежность создаваемых систем технического зрения. 05.13.18 – математическое моделирование, численные методы и комплексы программ 3. Методы получения приближенных и точных эталонных решений задач, описывающих моделируемые системы, процессы и явления; разработка и обоснование методик и правил адаптации компьютерных моделей, их эффективного использования при прогнозах эволюции систем, процессов и явлений.

Основная специальность 15.13.01 – системный анализ, управление и обработка информации 1. Методы и алгоритмы решения задач системного анализа, оптимизации, управления, принятия решений и обработки информации. 2. Визуализация, трансформация и анализ информации на основе компьютерных методов обработки информации.

Сопутствующие специальности 14.00.19 – лучевая диагностика, лучевая терапия 1. Лучевая диагностика (традиционная рентгенография, компьютерная, магнитно-резонансная, позитронно-эмиссионная томография, ультразвуковая диагностика). Методы интервенционной диагностики (сосудистая и несосудистая).

<question type=»close» id=»037″>

• <text>01 Какой тег устанавливает перевод строки в том месте, где этот тег находится? </text>

• <answers type=»request»>

• <answer id=»313759″ right=»0″>
• <nl>
• </answer>

• <answer id=»313760″ right=»1″>
• <br>
• </answer>

• <answer id=»313761″ right=»0″>
• <enter>
• </answer>

• <answer id=»313762″ right=»0″>
• <tt>
• </answer>

• </answers>

• </question>

• <question type=»close» id=»537″>

• <text>02 Как расшифровывается аббревиатура FTP?</text>

• <answers type=»request»>

• <answer id=»313759″ right=»0″>
• File Transfer Program </answer>

• <answer id=»313760″ right=»1″>
• File Transfer Protocol </answer>

• <answer id=»313761″ right=»0″>
• File TCP/IP Program </answer>

• <answer id=»313762″ right=»0″>
• File Type Protocol </answer>

• </answers>

• </question>

Список литературы к выпускной работе

[Электронный ресурс]//URL: https://pravsob.ru/diplomnaya/registratsiya-meditsinskih-izobrajeniy/

1. Сайт Высшей аттестационной комиссии Республики Беларусь. [Электронный ресурс] –

2. Недзьведь А.М., Абламейко С.В., Белоцерковский А.М., Лемман Т. Быстрый метод выделения сети сосудов на полутоновых ангиографических изображениях. – Искусственный интеллект. 2, 2006, С. — 206-210.

3. H. Blum. A Transformation for Extraction New Descriptors of Shape, Models for the Perception of Speech and Visual Form, MIT Press, 1967.

4. W. Gong and G. Bertrand. A simple parallel 3D thinning algorithm. Proc. IEEE Pattern Recognition, 188-190, 1990.

5. A. Lieutier. Any open bounded subset of Rn has the same homotopy typethan its medial axis, Proc. ACM SMI, 2003.

6. T.Y. Kong, A. Rosenfeld. Digital topology: Introduction and survey. Comp. Vision, Graphics, and Image Proc., 48(3):357-393, 1989.

7. D. Attali, J.-D. Boissonnat, H. Edelsbrunner. Stability and Computation of the medial axis — a State-of-the-Art Report, Mathematical Foundations of Scientific Visualization, Computer Graphics, and Massive Data Exploration, Springer-Verlag, 2004.

8. S.W. Choi, H.P. Seidel. Linear One-sided Stability of MAT for Weakly Injective 3D Domain, Proc. ACM SMA, 2002.

9. P.K. Saha, B.B. Chaudhuri. 3D Digital Topology under Binary Transformation with Applications, Computer Vision and Image Understanding, 63(3):418–429, 1996.

10. S. Svensson, C. Arcelli, G. Sanniti di Baja. Finding cavities and tunnels in 3D complex objects, Proc. ICIAP, pp. 342 – 347, 2003.

11. G. Sanniti di Baja, S. Svensson. A New Shape Descriptor for Surfaces in 3D Images, Pattern Recognition Letters, 23:703, 2002.

12. N. Gagvani and D. Silver. Parameter Controlled Volume Thinning, Graphical Models and Image Processing, 61(3):149-164, 1999.

13. C.W. Niblack, P.B. Gibbons, D.W. Capson. Generating skeletons and centerlines from the distance transform, Graphical Models and Image Processing, 54(5):420-437, 1992.

14. N. Gagvani and D. Silver. Animating volumetric models, Academic Press Professional 63(6):443-458, 2001.

15. D.-G. Kang, J.B. Ra. A New Path Planning Algorithm for MaximizingVisibility in Computed Tomography Colonography,

16. N. Cornea, D. Silver, X. Yuan, R. Balasubramanian. Computing Hierarchical Curve-Skeletons of 3D Objects, The Visual Computer, 21(11):945-955, 2005.

17. D.G. Morgenthaler. Three-dimensional simple points: serial erosion, parallel thinning and skeletonization, TR-1005, Computer Vision Lab., Univ. of Maryland, 1981.

18. Cornea, Nicu D., Silver D. and Min P. Curve-Skeleton Properties, Applications, and Algorithms // IEEE Transactions on Visualization and Computer Graphics. – 2007. Vol. 3, №13. – P. 530-548.

19. T.Y. Kong, A. Rosenfeld. Digital topology: Introduction and survey. Comp. Vision, Graphics, and Image Proc., 48(3):357-393, 1989.

20. G.J. Brostow, I. Essa, D. Steedly, V. Kwatra. Novel Skeletal Representation for Articulated Creatures, Proc. ECCV, 2004.

21. C.-M. Ma, S.-Y. Wan. A medial-surface oriented 3D two-subfield thinning algorithm, Pattern Recognition Letters, 22:1439, 2001.

22. C.M. Ma and M. Sonka. A fully parallel 3D thinning algorithm and its applications. Computer Vision and Image Understanding, 64(3):420-433, 1996.

23. H. Blum, R.N. Nagel. Shape description using weighted symmetric axis features, Pattern Recognition 10(3):167, 1978.

24. G. Borgefors, I. Nyström, G. Sanniti di Baja. Computing skeletons in three dimensions, Pattern Recognition, 32(7), 1999.

Pattern Recognition Letters

Computer Vision and Image Understanding

SIAM Review

28. Meijster, J.B.T.M. Roerdink, and W. H. Hesselink: A General Algorithm for Computing Distance Transforms in Linear Time, 1999

29. M. Couprie and R. Zrour. Discrete Bisector Function and Euclidean Skeleton, Lecture Notes in Computer Science, vol. 3429, 2005.

30. Bitter, A.E. Kaufman, M. Sato. Penalized-Distance Volumetric Skeleton Algorithm, IEEE TVCG, 7(3), 2001.

31. S. Bouix, K. Siddiqi. Divergence-Based Medial Surfaces, ECCV 1842:603-618, Springer-Verlag, 2000.

32. N. Gagvani and D. Silver. Parameter Controlled Volume Thinning,Graphical Models and Image Processing, 61(3):149-164, 1999.

33. H. Sundar, D. Silver, N. Gagvani, S. Dickinson. Skeleton Based Shape Matching and Retrieval, Proc. Shape Modeling Int’l, 2003.

34. T. He, L. Hong, D. Chen, Z. Liang. Reliable Path for Virtual Endoscopy: Ensuring Complete Examination of Human Organs, IEEE Trans. Visualization and Comp. Graphics, 7(4):333-342, 2001.

35. J.W. Brandt, V.R. Alazi. Continuous Skeleton Computation by Voronoi Diagram, CVGIP: Image Understanding, 55:329-338, 1992

36. F.-C. Wu, W.-C. Ma, R.-H. Liang, B.-Y. Chen, M. Ouhyoung. Domain connected graph: the skeleton of a closed 3D shape for animation, The Visual Computer 22(2):117, 2006.

37. T.K. Dey, J. Sun. Defining and computing curve-skeletons with medial geodesic function, Proc. Eurographics Symp. On Geometry Proc., 2006.

38. N. Ahuja, J. Chuang. Shape Representation Using a Generalized Potential Field Model, IEEE PAMI, 19(2): 169-176, 1997.

39. J. Chuang, C. Tsai, Min-Chi Ko. Skeletonization of Three-Dimensional Object Using Generalized Potential Field, IEEE PAMI, 22(11):1241,2000.

40. S. Katz, A. Tal. Hierarchical mesh decomposition using fuzzy clustering and cuts, Proc. ACM SIGGRAPH 2003.

41. P. Shilane, P. Min, M. Kazhdan, T. Funkhouser. The Princeton Shape Benchmark, Shape Modeling International, 2004.

42. Ф. Препарата, М. Шеймос. Вычислительная геометрия: Введение. — М.: Мир, 1989. Стр. 295

43. H. Atoui, S. Miguet and D. Sarrut. A fast morphing-based interpolation for medical images: application to conformal radiotherapy // Image Analysis and Stereology, – 2006, 25, P. 95 – 103.
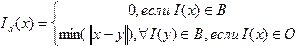